Die Tabelle 140 zeigt die wesentlichen Eingabedaten für das Beispielnetz. Wählt man bei der Suche folgende Parameter, dann werden in einer einzigen äußeren Iteration alle 3 denkbaren Routen gefunden:
- Anzahl Suchiterationen = 5
- σ= 8 • R0.5
- Die Widerstände der Netzobjekte werden für die alternativen Kurzwegsuchen gegenüber den „objektiven“ Widerständen (aus der Widerstandsdefinition und CR-Funktion) verändert. Sie werden jeweils zufällig aus einer Normalverteilung gezogen, deren Mittelwert der objektive Widerstand R ist und deren Standardabweichung σ als Funktion von R gegeben ist.
|
StrNr |
Typ |
v0 [km/h] |
Länge [m] |
Kapazität [Pkw-E] |
R0* [min] |
R0* [s] |
|
1 |
20 |
100 |
5 000 |
1 200 |
03:00 |
180 |
|
2 |
20 |
100 |
5 000 |
1 200 |
03:00 |
180 |
|
3 |
20 |
100 |
5 000 |
1 200 |
03:00 |
180 |
|
5 |
20 |
100 |
5 000 |
1 200 |
03:00 |
180 |
|
6 |
20 |
100 |
5 000 |
1 200 |
03:00 |
180 |
|
7 |
20 |
100 |
5 000 |
1 200 |
03:00 |
180 |
|
8 |
30 |
80 |
16 000 |
800 |
12:00 |
720 |
|
9 |
30 |
80 |
5 000 |
800 |
03:45 |
225 |
|
10 |
40 |
60 |
10 000 |
500 |
10:00 |
600 |
|
11 |
40 |
60 |
5 000 |
500 |
05:00 |
300 |
Im Anschluss an die Suche wird der Korrekturfaktor für die Eigenständigkeit jeder Route nach Cascetta bestimmt. Er ergibt sich aus der Ähnlichkeit der einzelnen Routenpaare bezüglich der Zeit t0 oder der Länge. Die Tabelle 141 zeigt die Commonality-Faktoren C. Daraus errechnet sich der Korrekturfaktor CFr der Route r.
- Route 1
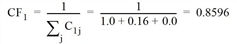
- Route 2
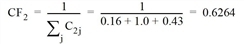
- Route 3
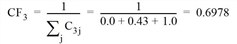
Aus dem Korrekturfaktor nach Cascetta und dem Widerstand Rmin0 im unbelasteten Netz errechnet sich der Anteil für jede Route.
Für Route 1 berechnet sich der Anteil unter Verwendung des Logit-Modells wie folgt.
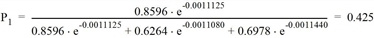
Analog ergeben sich die in der Tabelle 142 dargestellten Anteile für Route 2 und 3. Aus dem Produkt von Anteil P und Nachfrage F ergibt sich die Belastung jeder Route qr1 im ersten Iterationsschritt. Für Route 1 ergibt sich daher 0,425 • 2000 = 849,4 Pkw-E. Aus den Routenbelastungen können dann die Streckenbelastungen und damit die Netzwiderstände ermittelt werden (Abbildung 110). So ergeben sich die Widerstände R1 der Routen. Diese Zwischenergebnisse können in Visum nachvollzogen werden, wenn Sie in den Umlegungsparametern die maximale Anzahl der inneren Iterationen auf M = 1 setzen.
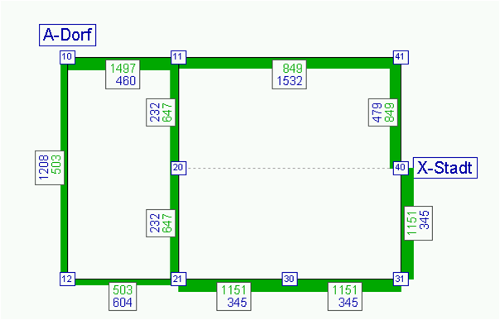
Abbildung 110: Belastungen und Streckenfahrzeiten nach dem ersten inneren Iterationsschritt m = 1
Für die Routenwahl im zweiten Iterationsschritt wird ein geschätzter Widerstand Rmin1 ermittelt. Da Δ = 0,5 ist, ergibt sich dieser Widerstand aus der Mittelwertbildung von Rmin0 und R1. Auf der Basis von Rmin1 erfolgt dann wieder wie im ersten Iterationsschritt die Aufteilung auf die 3 Routen. Für jede Route erhält man das Zwischenergebnis qr2’. Zur Glättung der Belastungen zwischen zwei Iterationsschritten wird die MSA-Methode (Method of Successive Averages) verwendet.
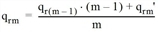
Für m = 2 ergibt sich für die Belastung der Route 1 folgendermaßen:
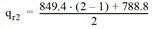
Diese Routenbelastung führt dann zu den Streckenbelastungen und Widerständen des zweiten Iterationsschrittes (Tabelle 143). Die Iterationen werden so lange fortgeführt, bis die Abbruchkriterien erfüllt sind.

